Class Activity (Resonant Circuits and Filters)

Series and parallel resonant circuit have an important role in electronic communication systems. In a

series resonant circuit magnitude of Xl is equal with magnitude of Xc. Therefore, impedance

decreasing and current increasing.





ωL = 1/ωC , ω₀^2 = 1 / (LC) ,   2πfo = ω<sub>0 , fo is resonant frequency of a series circuit. Under resonant 

condition circuit is purely resistive. So Z = R and current increasing because I = V/R .</sub>

Average power at resonant frequency is P(avg) = (Vm)^2 / (2R) .

 At a certain frequencies ω = ω ₁ , ω ₂ , called the half-power

frequencies the dissipated power is half the maximum value.

P(ω₁) = P(ω₂) = (Vm/radical(2))^2  / 2R = (Vm)^2 / (4R) .   ω₀² = ω₁* ω₂

B is a half-power bandwidth     B = ω ₂ − ω ₁

_{Q = 2(pi) (peak energy stored in the circuit)/(energy dissipated by the circuit in one period at resonance)}

The quality factor of a circuit in resonant:   Q = (ωoL)/R , B = R/L = ωo / Q

Changes of Q Relative to Resistance

High-Q circuits are used often in communications networks.

                                                       ω₁ ≈ ωo - (B/2)  ,   ω₂ ≈ ωo + (B/2) 

Parallel Circuit resonant

In contrast with a series circuit, in parallel circuit impedance is maximum and current is minimum.

 A filter is a circuit that design to select a specific frequency and reject others. 

1. A low-pass filter (LPF) passes low frequencies and stops high frequencies.

A Low pass RC Circuit

Transfer function for a RC series low pass filter.

When f is low, XC is high and Vc = Vout is maximum. When f is high, XC is minimum 

and Vc = Vout is minimum.

When f is low, XL is low and VR = Vout is maximum. When f is high, XL is maximum 

and VR = Vout is minimum.

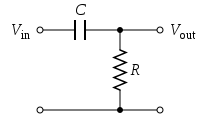
2. A high-pass filter (HPF) passes high frequencies and rejects low frequencies.

When f is low, XC is high and VR = Vout is minimum. When f is 

high, XC is minimum and VR= Vout is maximum.

When f is low, XL is low and VL = Vout is minimum. When f is 

high, XL is maximum and VL = Vout is maximum.

3. A band-pass filter (BPF) passes frequencies within a frequency band and blocks or attenuates

frequencies outside the band.

This is a series RLC circuit. In resonant frequency Z = R and current is 

maximum so VR = Vout is also maximum.

4. A band-stop filter (BSF) passes frequencies outside a frequency band and blocks or attenuates

frequencies within the band

.

This is a series RLC circuit. In resonant frequency Z = R and current is 

maximum so VR is maximum, and Vout is minimum.

Signals with Multiple Frequency Components

In this lab, the magnitude response of an electrical circuit is calculated  and this results is used 

to infer the effect of the circuit on some relatively complex input signals. In particular, the 

following input signal types  are applied to the circuit:

·       A signal composed of multiple sinusoidal waves of different frequencies

20[sin(1000πt) + sin(2000πt) + sin(20,000πt)]

·       A sinusoidal signal with a time-varying frequency (a sinusoidal sweep)

Figure 1: Calculation of Output Voltage

Figure 2: Calculation of Transfer Function

Figure 3: Multiple Sinusoidal Waves with Different Frequencies 

Figure 4: A Sinusoidal Sweep Wave 

Figure 5: Response of Circuit 

When frequency goes toward infinity, Xc goes toward zero. This means (Vout/Vin) will go 

to zero. When frequency goes toward zero, Xc goes toward infinity. This means (Vout/Vin) 

will go toward half. The response of circuit by H(ω) will determine.

Figure 6: A Schematic of the Circuit

Op Amp Relaxation Oscilator

        The first relaxation oscillator circuit, the astable multivibrator, was invented by Henri Abraham and Eugene Bloch using vacuum tubes during World War I. Balthasar van der Pol first distinguished relaxation oscillations from harmonic oscillations, originated the term "relaxation oscillator", and derived the first mathematical model of a relaxation oscillator, the influential Van der Pol oscillator model, in 1920. Van der Pol borrowed the term relaxation from mechanics; the discharge of the capacitor is analogous to the process of stress relaxation, the gradual disappearance of deformation and return to equilibrium in a inelastic medium. Relaxation oscillators can be divided into two classes.

 A) Saw tooth, sweep, or fly back oscillator.            B) Astable Multivibrator

Figure 1: A Relaxation Oscillator

Figure 2: A Relaxation Oscillator

Figure 3: Output Voltage and Capacitor Voltage

According to above graph frequency is 166.6 Hz.

percent frequency error = [(166.6 - 158)/166.6]*100% = 5.16%

Resistors have a little error and those effect on the other parameters.

Figure 4: A schematic of Relaxation Oscillator

Phasors Passive RL Circuit Response

          In this lab, the steady-state response of an electrical circuits is determined with a 

sinusoidal inputs.The input and output signals both have the same frequency, but the two

 signals can have different amplitudes and phase angles. The analysis of the circuit can be simplified 

by representing the sinusoidal signals as phasors. 

     Elements of series RL circuit are : L = 1mH and R = 47W.Input voltage frequencies:·        w = w_c /10 (low frequency input)
·        w = 10*w_c  (high frequency input)
·        w = w_c  (corner frequency input)

Figure 1: A Series RL Circuit

When frequency increasing the inductor voltage increasing and also phase difference between VL 

and VR, or between VL and I increase because VR is constant under frequency changes. Voltage 

across resistor in in phase with current circuit.

Figure 2: RL series at 1 KHz 

The phase difference is so small in above figure at 1 KHz.

Figure 3: RL Series at 7.1 KHz

The phase difference is so small in above figure at 1 KHz. According to the above grapg, frequency 

is equal with 7.1 KHz.  f = 1 / (140 μs) = 7143 Hz

Also ∆t = (2.5)*(5 μs) = 7.5 μs so ∆φ = (∆t / T) *(360°) , ∆φ = (7.5 / 140)*(360°) = 19.29°

 

Figure 4: A Schematic of  a Series RL Circuit

Class Activity (Week 12)

        Instantaneous, effective, and average power were discussed.

v(t) = Vm cos(ωt + θv) ,  i(t) = Im cos(ωt + θi)  or v(t) = Vm cos(ωt + θv - θi ) ,  i(t) = Im cos(ωt)

Instantaneous power is   P(t) = v(t)*i(t)  ,  P(t) = Pavg + Pavg cos(2ωt) - Pavg sin(2ωt) 

Average (Real) Power Pavg =  [(Vm*Im)/2] cos(θv - θi) = Vrms Irms cos(θv - θi) = S cos(θv - θi)

S is apparent power. Pf = Pavg / S = cos(θv - θi)

Reactive Power Q = [(Vm*Im)/2] sin(θv - θi)   

For resistive loads Q = 0 (Pf = 1) , For capacitive loads Q ˂ 0 (leading Pf) , 

For inductive loads Q  ˃ 0 (lagging Pf)

Figure 1: Effective or RMS Power

Vrms = Vm / √2   ,  Irms = Im / √2

Figure 2: Average Power

Figure 3: Apparent Power

S is apparent power. Pf = Pavg / S = cos(θv - θi)

Power Factor  Pf = cos(θv - θi)  ,  Reactive Power rf = sin(θv - θi) 

Lagging power factor shows that current lags voltage - hence an inductive load. 

Leading power factor shows that current leads voltage - hence a capacitive load.

Figure 4: Complex Power

Complex Power S (VA) = P (W) + jQ(VAR)  

P = (Ieff)^2 . R = (Veff)^2  / R   , Q = (Ieff)^2 . X = (Veff)^2  / X 

S = (Vrms).(Irms)* S = (V.I*)/2    ,    S = (Vrms * Irms) ˂(θv - θi) 

Figure 5: Power Triangle
(θv - θi) ˃ 0  Lagging power factor  ,  (θv - θi) ˃ 0  Lagging ˂ 0 Leading power factor

Figure 6: Impedance and Angel Phase

The power factor angle is equal to the angle of the load impedance, if V is the voltage across the load 

and I is current through the load.

Z = V˂θv  / I˂θi = (Vm / Im) ˂(θv - θi)  ,    Z = (Vrms / Irms) ˂(θv - θi)  

Figure 7: An Inductor Load (Lagging Power Factor)

Q = ((0.707*210)^2) / (2π*50*0.5) = 140.4 VAR

Figure 8: An Example

FREQUENCY DEPENDANCE AND TRANSFER FUNCTIONS

        The frequency response of a circuit may also be considered as the variation of the gain and phase with

frequency. The transfer function H(ω) (network function) is a useful analytical tool for finding

the frequency response of a circuit. In fact, the frequency response of a circuit is the plot of the circuit’s

transfer function H(ω) versus ω, with ω varying from ω = 0 to ω = ∞. 

H(ω) = Voltage gain = Vo(ω) / Vi(ω)    ,  H(ω) = Current gain = Io(ω) / Ii(ω) 

H(ω) = Transfer Impedance = Vo(ω) / Ii(ω)   , H(ω) = Transfer Admittance = Io(ω) / Vi(ω)  

 H(ω) = H(ω) φ. H(ω) = N(ω) / D(ω) . 

The roots of transfer function are determined when N(ω) = 0.  

 The poles of transfer function are determined when D(ω) = 0.

Figure 9: Zeros and Poles of a Series RLC

Figure 10: Zeros and Poles of a Parallel Circuit

Figure 11